Exercise 2.1
1. The graphs y = p(x) are given in the following figure, for some polynomials p(x). Find the number of zeros of p(x), in each case.
Solution:
(i)
The number of zeros is 0 as the graph does not intersect the x-axis at any point.
(ii)
The number of zeros is 1 as the graph intersects x-axis at only one point.
(iii)
The number of zeros is 3 as the graph intersects x-axis at 3 points.
(iv)
The number of zeros is 2 as the graph intersects x-axis at 2 points.
(v)
The number of zeros is 4 as the graph intersects x-axis at 4 points.
(vi)
The number of zeros is 3 as the graph intersects x-axis at 3 points.
Exercise 2.2:
1. Find the zeros of the following quadratic polynomials and verify the relationship between the zeros and coefficients.
(i) x² ˗ 2x ˗ 8
(ii) 4s² ˗ 4s + 1
(iii) 6x² ˗ 3 ˗ 7x
(iv) 4u² + 8u
(v) t² ˗ 15
(vi) 3x² ˗ x ˗ 4
Solution:
(i)
x² ˗ 2x ˗ 8 = x² ˗ 4x + 2x ˗ 8 [ ˗ 4 + 2 = ˗ 2 and ˗ 4 × 2 = ˗ 8 ]
= x(x ˗ 4) + 2(x ˗ 4)
= (x ˗ 4)(x + 2)
To find the zero, equate the polynomial to 0.
(x ˗ 4)(x + 2) = 0
⇒ x = 4 and x = ˗ 2.
Hence the zeros of x² ˗ 2x ˗ 8 is 4 and ˗ 2.
Verifying the relationship between zeros and coefficients.
(ii)
4s² ˗ 4s + 1 = ( 2s ˗ 1 )²
To find the zero, equate the polynomial to 0.
( 2s ˗ 1 )² = 0
⟹ ( 2s ˗ 1 )( 2s ˗ 1 ) = 0
Verifying the relationship between zeros and coefficients.
(iii)
6x² ˗ 3 ˗ 7x = 6x² ˗ 7x ˗ 3
= 6x² + 2x ˗ 9x ˗ 3 [ 2 ˗ 9 = ˗7 and 2 × ( ˗ 9 ) = ˗ 18 ]
= 2x(3x + 1) ˗ 3(3x + 1)
= (3x + 1)(2x ˗ 3)
To find the zero, equate the polynomial to 0.
Verifying the relationship between zeros and coefficients.
(iv)
4u² + 8u = 4u(u + 2 )
To find the zero, equate the polynomial to 0.
4u(u + 2 ) = 0
4u = 0 and u + 2 = 0
u = 0 and u = ˗2
Verifying the relationship between zeros and coefficients.
(v)
t² ˗ 15 = ( t + √15 ) ( t ˗ √15 )
To find the zero, equate the polynomial to 0.
( t + √15 ) ( t ˗ √15 ) = 0
t + √15 = 0 and t ˗ √15 = 0
t = ˗√15 and t = √15
Verifying the relationship between zeros and coefficients.
(vi)
3x² ˗ x ˗ 4 = 3x² + 3x ˗ 4x ˗ 4
= 3x( x + 1 ) ˗4( x + 1 )
= ( x + 1 ) ( 3x ˗ 4 )
To find the zero, equate the polynomial to 0.
( x + 1 ) ( 3x ˗ 4 ) = 0
x + 1 = 0 and 3x ˗ 4 = 0
x = ˗1 and 3x = 4
Verifying the relationship between zeros and coefficients.
2. Find a quadratic polynomial each with the given numbers as the sum and product of its zeroes respectively.
Solution:
(i)
Let the polynomial be ax² + bx + c and its zeroes be ⍺ and β.
∴ a = 4 , b = ˗1 and c = ˗4.
Hence the quadratic polynomial is 4x² ˗ x ˗ 4.
(ii)
Let the polynomial be ax² + bx + c and its zeroes be ⍺ and β.
∴ a = 3, b = ˗3√2 and c = 1.
Hence the quadratic polynomial is 3x² ˗ 3√2x + 1.
(iii)
Let the polynomial be ax² + bx + c and its zeroes be ⍺ and β.
∴ a = 1 , b = 0 and c = √5.
Hence the quadratic polynomial is x² + √5.
(iv)
Let the polynomial be ax² + bx + c and its zeroes be ⍺ and β.
∴ a = 1, b = ˗1 and c = 1
Hence the quadratic polynomial is x² ˗ x + 1.
(v)
Let the polynomial be ax² + bx + c and its zeroes be ⍺ and β.
∴ a = 4, b = 1 and c = 1.
Hence the quadratic polynomial is 4x² + x + 1.
(vi)
Let the polynomial be ax² + bx + c and its zeroes be ⍺ and β.
∴ a = 1, b = ˗4 and c = 1.
Hence the quadratic polynomial is x² ˗ 4x + 1.
Exercise 2.3:
1. Divide the polynomial p(x) by the polynomial g(x) and find the quotient and remainder in each of the following.
(i)
p(x) = x³ ˗ 3x² + 5x ˗ 3, g(x) = x² ˗ 2.
Solution:
∴ Quotient = x ˗ 3 and Remainder = 7x ˗ 9.
(ii)
p(x) = x⁴ ˗ 3x² + 4x + 5, g(x) = x² + 1 ˗ x
Solution:
∴ Quotient = x² + x ˗ 3 and Remainder = 8
(iii)
p(x) = x⁴ ˗ 5x + 6, g(x) = 2 ˗ x²
Solution:
∴ Quotient = ˗x² ˗2 and Remainder = ˗5x + 10
2. Check whether the first polynomial is a factor of the second polynomial by dividing the second polynomial by the first polynomial.
(i) t² ˗ 3, 2t⁴ + 3t³ ˗ 2t² ˗ 9t ˗ 12
Solution:
The remainder is 0 while dividing 2t⁴ + 3t³ ˗ 2t² ˗ 9t ˗ 12 by t² ˗ 3.
∴ t² ˗ 3 is a factor of 2t⁴ + 3t³ ˗ 2t² ˗ 9t ˗ 12.
(ii) x² + 3x + 1, 3x⁴ + 5x³ – 7x² + 2x + 2
The remainder is 0 while dividing 3x⁴ + 5x³ – 7x² + 2x + 2 by x² + 3x + 1.
Hence x² + 3x + 1 is a factor of 3x⁴ + 5x³ – 7x² + 2x + 2.
(iii) x³ – 3x + 1, x⁵ – 4x³ + x² + 3x + 1
Solution:
The remainder is 0 while dividing x⁵ – 4x³ + x² + 3x + 1 by x³ – 3x + 1.
Hence x³ – 3x + 1 is a factor of x⁵ – 4x³ + x² + 3x + 1.
3. Obtain all other zeroes of 3x⁴ + 6x³ – 2x² – 10x – 5, if two of its zeroes are √(5/3)
and –√(5/3).
Solution:
p(x) = 3x⁴ + 6x³ – 2x² – 10x – 5
Since the two zeroes are √(5/3) and –√(5/3).
To find the other zeros we equate (x + 1)² to 0.
(x + 1)² = 0
(x + 1)(x + 1) = 0
x = ˗1 and ˗1.
Hence the zeroes of the given polynomial are √(5/3), –√(5/3), ˗1 and ˗1.
4. On dividing x³ ˗ 3x² + x + 2 by a polynomial g(x), the quotient and remainder were x ˗ 2 and
˗2x + 4, respectively. Find g(x).
Solution:
Dividend = x³ ˗ 3x² + x + 2
Divisor = g(x) = ?
Quotient = x ˗ 2
Remainder = ˗2x + 4
We know that
Dividend = Quotient × Divisor + Remainder
x³ ˗ 3x² + x + 2 = (x ˗ 2) × g(x) + (˗2x + 4 )
(x ˗ 2) × g(x) = ( x³ ˗ 3x² + x + 2 ) ˗ (˗2x + 4 )
= x³ ˗ 3x² + x + 2 + 2x ˗ 4
= x³ ˗ 3x² + 3x ˗ 2
∴ g(x) = x² ˗ x + 1
5. Give examples of polynomial p(x), g(x), q(x) and r(x), which satisfy the division algorithm and
(i) deg p(x) = deg q(x)
(ii) deg q(x) = deg r(x)
(iii) deg r(x) = 0
Solution:
(i)
Let us assume the division of 6x² + 2x + 2 by 2
Here, p(x) = 6x² + 2x + 2
g(x) = 2
q(x) = 3x² + x + 1
r(x) = 0
Degree of p(x) and q(x) is same i.e. 2.
Checking for division algorithm,
p(x) = g(x) × q(x) + r(x)
Or, 6x² + 2x + 2 = 2 × (3x² + x + 1) + 0
= 6x² + 2x + 2
Hence, division algorithm is satisfied.
(ii)
Let us assume the division of x³ + x by x²,
Here, p(x) = x³ + x
g(x) = x²
q(x) = x and r(x) = x
Clearly, the degree of q(x) and r(x) is the same i.e., 1.
Checking for division algorithm,
p(x) = g(x) × q(x) + r(x)
x³ + x = (x² ) × x + x
= x³ + x
Thus, the division algorithm is satisfied.
(iii)
Let us assume the division of x³ + 1 by x².
Here, p(x) = x³ + 1
g(x) = x²
q(x) = x and r(x) = 1
Clearly, the degree of r(x) is 0.
Checking for division algorithm,
p(x) = g(x) × q(x) + r(x)
x³ + 1 = (x² ) × x + 1
= x³ + 1
Thus, the division algorithm is satisfied.
1. The graphs y = p(x) are given in the following figure, for some polynomials p(x). Find the number of zeros of p(x), in each case.
(i)
The number of zeros is 0 as the graph does not intersect the x-axis at any point.
(ii)
The number of zeros is 1 as the graph intersects x-axis at only one point.
(iii)
The number of zeros is 3 as the graph intersects x-axis at 3 points.
(iv)
The number of zeros is 2 as the graph intersects x-axis at 2 points.
(v)
The number of zeros is 4 as the graph intersects x-axis at 4 points.
(vi)
The number of zeros is 3 as the graph intersects x-axis at 3 points.
Exercise 2.2:
1. Find the zeros of the following quadratic polynomials and verify the relationship between the zeros and coefficients.
(i) x² ˗ 2x ˗ 8
(ii) 4s² ˗ 4s + 1
(iii) 6x² ˗ 3 ˗ 7x
(iv) 4u² + 8u
(v) t² ˗ 15
(vi) 3x² ˗ x ˗ 4
Solution:
(i)
x² ˗ 2x ˗ 8 = x² ˗ 4x + 2x ˗ 8 [ ˗ 4 + 2 = ˗ 2 and ˗ 4 × 2 = ˗ 8 ]
= x(x ˗ 4) + 2(x ˗ 4)
= (x ˗ 4)(x + 2)
To find the zero, equate the polynomial to 0.
(x ˗ 4)(x + 2) = 0
⇒ x = 4 and x = ˗ 2.
Hence the zeros of x² ˗ 2x ˗ 8 is 4 and ˗ 2.
Verifying the relationship between zeros and coefficients.
(ii)
4s² ˗ 4s + 1 = ( 2s ˗ 1 )²
To find the zero, equate the polynomial to 0.
( 2s ˗ 1 )² = 0
⟹ ( 2s ˗ 1 )( 2s ˗ 1 ) = 0
Verifying the relationship between zeros and coefficients.
(iii)
6x² ˗ 3 ˗ 7x = 6x² ˗ 7x ˗ 3
= 6x² + 2x ˗ 9x ˗ 3 [ 2 ˗ 9 = ˗7 and 2 × ( ˗ 9 ) = ˗ 18 ]
= 2x(3x + 1) ˗ 3(3x + 1)
= (3x + 1)(2x ˗ 3)
To find the zero, equate the polynomial to 0.
Verifying the relationship between zeros and coefficients.
(iv)
4u² + 8u = 4u(u + 2 )
To find the zero, equate the polynomial to 0.
4u(u + 2 ) = 0
4u = 0 and u + 2 = 0
u = 0 and u = ˗2
Verifying the relationship between zeros and coefficients.
(v)
t² ˗ 15 = ( t + √15 ) ( t ˗ √15 )
To find the zero, equate the polynomial to 0.
( t + √15 ) ( t ˗ √15 ) = 0
t + √15 = 0 and t ˗ √15 = 0
t = ˗√15 and t = √15
Verifying the relationship between zeros and coefficients.
(vi)
3x² ˗ x ˗ 4 = 3x² + 3x ˗ 4x ˗ 4
= 3x( x + 1 ) ˗4( x + 1 )
= ( x + 1 ) ( 3x ˗ 4 )
To find the zero, equate the polynomial to 0.
( x + 1 ) ( 3x ˗ 4 ) = 0
x + 1 = 0 and 3x ˗ 4 = 0
x = ˗1 and 3x = 4
Verifying the relationship between zeros and coefficients.
2. Find a quadratic polynomial each with the given numbers as the sum and product of its zeroes respectively.
Solution:
(i)
Let the polynomial be ax² + bx + c and its zeroes be ⍺ and β.
Hence the quadratic polynomial is 4x² ˗ x ˗ 4.
(ii)
Let the polynomial be ax² + bx + c and its zeroes be ⍺ and β.
∴ a = 3, b = ˗3√2 and c = 1.
Hence the quadratic polynomial is 3x² ˗ 3√2x + 1.
(iii)
Let the polynomial be ax² + bx + c and its zeroes be ⍺ and β.
∴ a = 1 , b = 0 and c = √5.
Hence the quadratic polynomial is x² + √5.
(iv)
Let the polynomial be ax² + bx + c and its zeroes be ⍺ and β.
∴ a = 1, b = ˗1 and c = 1
Hence the quadratic polynomial is x² ˗ x + 1.
(v)
Let the polynomial be ax² + bx + c and its zeroes be ⍺ and β.
∴ a = 4, b = 1 and c = 1.
Hence the quadratic polynomial is 4x² + x + 1.
(vi)
Let the polynomial be ax² + bx + c and its zeroes be ⍺ and β.
∴ a = 1, b = ˗4 and c = 1.
Hence the quadratic polynomial is x² ˗ 4x + 1.
Exercise 2.3:
1. Divide the polynomial p(x) by the polynomial g(x) and find the quotient and remainder in each of the following.
(i)
p(x) = x³ ˗ 3x² + 5x ˗ 3, g(x) = x² ˗ 2.
Solution:
∴ Quotient = x ˗ 3 and Remainder = 7x ˗ 9.
(ii)
p(x) = x⁴ ˗ 3x² + 4x + 5, g(x) = x² + 1 ˗ x
Solution:
∴ Quotient = x² + x ˗ 3 and Remainder = 8
(iii)
p(x) = x⁴ ˗ 5x + 6, g(x) = 2 ˗ x²
Solution:
2. Check whether the first polynomial is a factor of the second polynomial by dividing the second polynomial by the first polynomial.
(i) t² ˗ 3, 2t⁴ + 3t³ ˗ 2t² ˗ 9t ˗ 12
Solution:
The remainder is 0 while dividing 2t⁴ + 3t³ ˗ 2t² ˗ 9t ˗ 12 by t² ˗ 3.
∴ t² ˗ 3 is a factor of 2t⁴ + 3t³ ˗ 2t² ˗ 9t ˗ 12.
(ii) x² + 3x + 1, 3x⁴ + 5x³ – 7x² + 2x + 2
The remainder is 0 while dividing 3x⁴ + 5x³ – 7x² + 2x + 2 by x² + 3x + 1.
Hence x² + 3x + 1 is a factor of 3x⁴ + 5x³ – 7x² + 2x + 2.
(iii) x³ – 3x + 1, x⁵ – 4x³ + x² + 3x + 1
Solution:
The remainder is 0 while dividing x⁵ – 4x³ + x² + 3x + 1 by x³ – 3x + 1.
Hence x³ – 3x + 1 is a factor of x⁵ – 4x³ + x² + 3x + 1.
3. Obtain all other zeroes of 3x⁴ + 6x³ – 2x² – 10x – 5, if two of its zeroes are √(5/3)
and –√(5/3).
Solution:
p(x) = 3x⁴ + 6x³ – 2x² – 10x – 5
Since the two zeroes are √(5/3) and –√(5/3).
To find the other zeros we equate (x + 1)² to 0.
(x + 1)² = 0
(x + 1)(x + 1) = 0
x = ˗1 and ˗1.
Hence the zeroes of the given polynomial are √(5/3), –√(5/3), ˗1 and ˗1.
4. On dividing x³ ˗ 3x² + x + 2 by a polynomial g(x), the quotient and remainder were x ˗ 2 and
˗2x + 4, respectively. Find g(x).
Solution:
Dividend = x³ ˗ 3x² + x + 2
Divisor = g(x) = ?
Quotient = x ˗ 2
Remainder = ˗2x + 4
We know that
Dividend = Quotient × Divisor + Remainder
x³ ˗ 3x² + x + 2 = (x ˗ 2) × g(x) + (˗2x + 4 )
(x ˗ 2) × g(x) = ( x³ ˗ 3x² + x + 2 ) ˗ (˗2x + 4 )
= x³ ˗ 3x² + x + 2 + 2x ˗ 4
= x³ ˗ 3x² + 3x ˗ 2
∴ g(x) = x² ˗ x + 1
5. Give examples of polynomial p(x), g(x), q(x) and r(x), which satisfy the division algorithm and
(i) deg p(x) = deg q(x)
(ii) deg q(x) = deg r(x)
(iii) deg r(x) = 0
Solution:
(i)
Let us assume the division of 6x² + 2x + 2 by 2
Here, p(x) = 6x² + 2x + 2
g(x) = 2
q(x) = 3x² + x + 1
r(x) = 0
Degree of p(x) and q(x) is same i.e. 2.
Checking for division algorithm,
p(x) = g(x) × q(x) + r(x)
Or, 6x² + 2x + 2 = 2 × (3x² + x + 1) + 0
= 6x² + 2x + 2
Hence, division algorithm is satisfied.
(ii)
Let us assume the division of x³ + x by x²,
Here, p(x) = x³ + x
g(x) = x²
q(x) = x and r(x) = x
Clearly, the degree of q(x) and r(x) is the same i.e., 1.
Checking for division algorithm,
p(x) = g(x) × q(x) + r(x)
x³ + x = (x² ) × x + x
= x³ + x
Thus, the division algorithm is satisfied.
(iii)
Let us assume the division of x³ + 1 by x².
Here, p(x) = x³ + 1
g(x) = x²
q(x) = x and r(x) = 1
Clearly, the degree of r(x) is 0.
Checking for division algorithm,
p(x) = g(x) × q(x) + r(x)
x³ + 1 = (x² ) × x + 1
= x³ + 1
Thus, the division algorithm is satisfied.










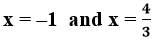



















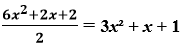


No comments:
Post a Comment