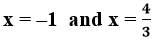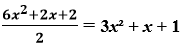Exercise 3.1:
1. Aftab tells his daughter, "Seven years ago, I was seven times as old as you were then. Also, three years from now, I shall be three times as old as you will be." (Isn't this interesting?) Represent this situation algebraically and graphically.
Solution:
Let present age of Aftab be x
And, present age of daughter is represented by y
Then Seven years ago,
Age of Aftab = x – 7
Age of daughter = y – 7
According to the question,
(x – 7) = 7 (y – 7 )
x – 7 = 7 y – 49
x – 7y = – 49 + 7
x – 7y = – 42 …(i)
x = 7y – 42
Putting y = 5, 6 and 7, we get
x = 7 × 5 – 42 = 35 – 42 = – 7
x = 7 × 6 – 42 = 42 – 42 = 0
x = 7 × 7 – 42 = 49 – 42 = 7
Three years from now ,
Age of Aftab = x +3
Age of daughter = y +3
According to the question,
(x + 3) = 3 (y + 3)
x + 3 = 3y + 9
x – 3y = 9–3
x – 3y = 6 …(ii)
x = 3y + 6
Putting, y = –2,–1 and 0, we get
x = 3 × – 2 + 6 = –6 + 6 =0
x = 3 × – 1 + 6 = –3 + 6 = 3
x = 3 × 0 + 6 = 0 + 6 = 6
Algebraic representation
From equation (i) and (ii)
x – 7y = – 42 …(i)
x – 3y = 6 …(ii)
Graphical representation
2. The coach of a cricket team buys 3 bats and 6 balls for Rs 3900. Later, she buys another bat and 3 more balls of the same kind for Rs 1300. Represent this situation algebraically and geometrically.
Solution:
Let cost of one bat = Rs x
Cost of one ball = Rs y
3 bats and 6 balls for Rs 3900 So that
3x + 6y = 3900 … (i)
Dividing equation by 3, we get
x + 2y = 1300
Subtracting 2y both side we get
x = 1300 – 2y
Putting y = –1300, 0 and 1300 we get
x = 1300 – 2 (–1300) = 1300 + 2600 = 3900
x = 1300 –2(0) = 1300 – 0 = 1300
x = 1300 – 2(1300) = 1300 – 2600 = – 1300
Given that she buys another bat and 2 more balls of the same kind for Rs 1300
So, we get
x + 2y = 1300 … (ii)
Subtracting 2y both side we get
x = 1300 – 2y
Putting y = – 1300, 0 and 1300 we get
x = 1300 – 2 (–1300) = 1300 + 2600 = 3900
x = 1300 – 2 (0) = 1300 – 0 = 1300
x = 1300 – 2(1300) = 1300 – 2600 = –1300
Algebraic representation
3x + 6y = 3900 … (i)
x + 2y = 1300 … (ii)
Graphical representation,
3. The cost of 2 kg of apples and 1 kg of grapes on a day was found to be Rs 160. After a month, the cost of 4 kg of apples and 2 kg of grapes is Rs 300. Represent the situation algebraically and geometrically.
Solution:
Let cost each kg of apples = Rs x
Cost of each kg of grapes = Rs y
Given that the cost of 2 kg of apples and 1kg of grapes on a day was found to be Rs 160
So that
2 x + y = 160 … (i)
2x = 160 - y
x = (160 – y)/2
Let y = 0 , 80 and 160, we get
x = (160 – ( 0 )/2 = 80
x = (160 – 80 )/2 = 40
x = (160 – 2 × 80)/2 = 0
Given that the cost of 4 kg of apples and 2 kg of grapes is Rs 300
So we get
4x + 2y = 300 … (ii)
Dividing by 2 we get
2x + y = 150
Subtracting 2x both side, we get
y = 150 – 2x
Putting x = 0 , 50 , 100 we get
y = 150 – 2 × 0 = 150
y = 150 – 2 × 50 = 50
y = 150 – 2 × (100) = –50
Algebraic representation,
2x + y = 160 … (i)
4x + 2y = 300 … (ii)
Graphical representation,
Exercise 3.2:
1. Form the pair of linear equations in the following problems, and find their solutions graphically.
(i) 10 students of Class X took part in a Mathematics quiz. If the number of girls is 4 more than the number of boys, find the number of boys and girls who took part in the quiz.
Solution:
Let number of boys = x
Number of girls = y
Given that total number of student is 10 so that
x + y = 10
Subtract y both side we get
x = 10 – y
Putting y = 0 , 5, 10 we get
x = 10 – 0 = 10
x = 10 – 5 = 5
x = 10 – 10 = 0
Given that If the number of girls is 4 more than the number of boys
So that
y = x + 4
Putting x = –4, 0, 4, and we get
y = – 4 + 4 = 0
y = 0 + 4 = 4
y = 4 + 4 = 8
Graphical representation
Both lines intersect at (3,7)
Hence the number of boys = 3 and number of girls = 7.
(ii) 5 pencils and 7 pens together cost Rs 50, whereas 7 pencils and 5 pens together cost Rs 46. Find the cost of one pencil and that of one pen.
Solution:
Let cost of pencil = Rs x
Cost of pens = Rs y
5 pencils and 7 pens together cost Rs 50,
So we get
5x + 7y = 50
Subtracting 7y both sides we get
5x = 50 – 7y
Dividing by 5 we get
Putting value of y = 5 , 10 and 15 we get
x = 10 – 7 × 5/5 = 10 – 7 = 3
x = 10 – 7 × 10/5 = 10 – 14 = – 4
x = 10 – 7 × 15/5 = 10 – 21 = – 11
Given that 7 pencils and 5 pens together cost Rs 46
7x + 5y = 46
Subtracting 7x both side we get
5y = 46 – 7x
Dividing by 5 we get
y = 9.2 – 1.4x
Putting x = 0 , 2 and 4 we get
y = 9.2 – 1.4 × 0 = 9.2 – 0 = 9.2
y = 9.2 – 1.4 (2) = 9.2 – 2.8 = 6.4
y = 9.2 – 1.4 (4) = 9.2 – 5.6 = 3.6
Graphical representation:
Both lines intersect at (3,5)
Hence the cost of one pencil = Rs 3 and cost of one pen = Rs 5.
2. On comparing the ratios a1/a2 , b1/b2 and c1/c2, find out whether the lines representing the following pairs of linear equations intersect at a point, are parallel or coincident.
(i) 5x – 4y + 8 = 0
7x + 6y – 9 = 0
Solution:
Comparing these equation with
a1x + b1y + c1 = 0
a2x + b2y + c2 = 0
We get
a1 = 5, b1 = –4, and c1 = 8
a2 =7, b2 = 6 and c2 = –9
a1/a2 = 5/7,
b1/b2 = –4/6 and
c1/c2 = 8/-9
Hence, a1/a2 ≠ b1/b2
Therefore, both are intersecting lines at one point.
(ii) 9x + 3y + 12 = 0
18x + 6y + 24 = 0
Comparing these equations with
a1x + b1y + c1 = 0
a2x + b2y + c2 = 0
We get
a1 = 9, b1 = 3, and c1 = 12
a2 = 18, b2 = 6 and c2 = 24
a1/a2 = 9/18 = 1/2
b1/b2 = 3/6 = 1/2 and
c1/c2 = 12/24 = 1/2
Hence, a1/a2 = b1/b2 = c1/c2
Therefore, both lines are coincident.
(iii) 6x – 3y + 10 = 0
2x – y + 9 = 0
Comparing these equations with
a1x + b1y + c1 = 0
a2x + b2y + c2 = 0
We get
a1 = 6, b1 = –3, and c1 = 10
a2 = 2, b2 = –1 and c2 = 9
a1/a2 = 6/2 = 3/1
b1/b2 = –3/–1 = 3/1 and
c1/c2 = 12/24 = 1/2
Hence, a1/a2 = b1/b2 ≠ c1/c2
Therefore, both lines are parallel.
3. On comparing the ratios a1/a2 , b1/b2 and c1/c2 find out whether the following pair of linear equations are consistent, or inconsistent.
(i) 3x + 2y = 5 ; 2x – 3y = 7
(ii) 2x – 3y = 8 ; 4x – 6y = 9
(iii) 3/2x + 5/3y = 7 ; 9x – 10y = 14
(iv) 5x – 3y = 11 ; – 10x + 6y = –22
(v) 4/3x + 2y =8 ; 2x + 3y = 12
Solution:
(i)
3x + 2y = 5 ; 2x – 3y = 7
a1/a2 = 3/2
b1/b2 = –2/3 and
c1/c2 = 5/7
Hence, a1/a2 ≠ b1/b2
These linear equations are intersecting each other at one point and thus have only one possible solution. Hence, the pair of linear equations is consistent.
(ii)
2x – 3y = 8 ; 4x – 6y = 9
a1/a2 = 2/4 = 1/2
b1/b2 = –3/–6 = 1/2 and
c1/c2 = 8/9
Hence, a1/a2 = b1/b2 ≠ c1/c2
Therefore, these linear equations are parallel to each other and thus have no possible solution. Hence, the pair of linear equations is inconsistent.
(iii)
3/2x + 5/3y = 7 ; 9x – 10y = 14
a1/a2 = 3/2/9 = 1/6
b1/b2 = 5/3/–10 = –1/6 and
c1/c2 = 7/14 = 1/2
Hence, a1/a2 ≠ b1/b2
Therefore, these linear equations are intersecting each other at one point and thus have only one possible solution. Hence, the pair of linear equations is consistent.
(iv)
5x – 3y = 11 ; – 10x + 6y = –22
a1/a2 = 5/-10 = -1/2
b1/b2 = -3/6 = -1/2 and
c1/c2 = 11/-22 = -1/2
Hence, a1/a2 = b1/b2 = c1/c2
Therefore, these linear equations are coincident pair of lines and thus have infinite number of possible solutions. Hence, the pair of linear equations is consistent.
4. Which of the following pairs of linear equations are consistent/inconsistent? If consistent, obtain the solution graphically:
(i) x + y = 5, 2x + 2y = 10
(ii) x – y = 8, 3x – 3y = 16
(iii) 2x + y – 6 = 0, 4x – 2y – 4 = 0
(iv) 2x – 2y – 2 = 0, 4x – 4y – 5 = 0
Solution:
x + y = 5; 2x + 2y = 10
a1/a2 = 1/2
b1/b2 = 1/2 and
c1/c2 = 5/10 = 1/2
Hence, a1/a2 = b1/b2 = c1/c2
Therefore, these linear equations are coincident pair of lines and thus have infinite number of possible solutions. Hence, the pair of linear equations is consistent.
x + y = 5
x = 5 – y
And, 2x + 2y = 10
x = 10 – 2y/2
Graphical representation:
(ii)
x – y = 8, 3x – 3y = 16
a1/a2 = 1/3
b1/b2 = –1/–3 = 1/3 and
c1/c2 = 8/16 = 1/2
Hence, a1/a2 = b1/b2 ≠ c1/c2
Therefore, these linear equations are parallel to each other and thus have no possible solution. Hence, the pair of linear equations is inconsistent.
(iii)
2x + y – 6 = 0, 4x – 2y – 4 = 0
a1/a2 = 2/4 = 1/2
b1/b2 = –1/2 and
c1/c2 = –6/–4 = 3/2
Hence, a1/a2 ≠ b1/b2
Therefore, these linear equations are intersecting each other at one point and thus have only one possible solution. Hence, the pair of linear equations is consistent.
2x + y – 6 = 0
y = 6 – 2x
And, 4x – 2y – 4 = 0
y = 4x – 4/2
Graphical representation:
From the figure, it can be observed that these lines are intersecting each other at the only one point i.e., (2,2) which is the solution for the given pair of equations.
5. Half the perimeter of a rectangular garden, whose length is 4 m more than its width, is 36 m. Find the dimensions of the garden.
Solution:
Let length of rectangle = x m
Width of the rectangle = y m
According to the question,
y – x = 4 ... (i)
y + x = 36 ... (ii)
y – x = 4
y = x + 4
y + x = 36
Graphical representation:
From the figure, it can be observed that these lines are intersecting each other at only point i.e., (16, 20). Therefore, the length and width of the given garden is 20 m and 16 m respectively.
6. Given the linear equation 2x + 3y – 8 = 0, write another linear equations in two variables such that the geometrical representation of the pair so formed is:
(i) intersecting lines
(ii) parallel lines
(iii) coincident lines
Solution:
(i) Intersecting lines:
For this condition,
a1/a2 ≠ b1/b2
The second line such that it is intersecting the given line is
2x + 4y – 6 = 0 as
a1/a2 = 2/2 = 1
b1/b2 = 3/4 and
a1/a2 ≠ b1/b2
(ii) Parallel lines
For this condition,
a1/a2 = b1/b2 ≠ c1/c2
Hence, the second line can be
4x + 6y – 8 = 0 as
a1/a2 = 2/4 = 1/2
b1/b2 = 3/6 = 1/2 and
c1/c2 = –8/–8 = 1
and a1/a2 = b1/b2 ≠ c1/c2
(iii) Coincident lines
For coincident lines,
a1/a2 = b1/b2 = c1/c2
Hence, the second line can be
6x + 9y – 24 = 0 as
a1/a2 = 2/6 = 1/3
b1/b2 = 3/9 = 1/3 and
c1/c2 = –8/–24 = 1/3
and a1/a2 = b1/b2 = c1/c2
7. Draw the graphs of the equations x – y + 1 = 0 and 3x + 2y – 12 = 0. Determine the coordinates of the vertices of the triangle formed by these lines and the x-axis, and shade the triangular region.
Answer
x – y + 1 = 0
x = y – 1
3x + 2y – 12 = 0
x = 12 – 2y/3
Graphical representation:
1. Aftab tells his daughter, "Seven years ago, I was seven times as old as you were then. Also, three years from now, I shall be three times as old as you will be." (Isn't this interesting?) Represent this situation algebraically and graphically.
Solution:
Let present age of Aftab be x
And, present age of daughter is represented by y
Then Seven years ago,
Age of Aftab = x – 7
Age of daughter = y – 7
According to the question,
(x – 7) = 7 (y – 7 )
x – 7 = 7 y – 49
x – 7y = – 49 + 7
x – 7y = – 42 …(i)
x = 7y – 42
Putting y = 5, 6 and 7, we get
x = 7 × 5 – 42 = 35 – 42 = – 7
x = 7 × 6 – 42 = 42 – 42 = 0
x = 7 × 7 – 42 = 49 – 42 = 7
Three years from now ,
Age of Aftab = x +3
Age of daughter = y +3
According to the question,
(x + 3) = 3 (y + 3)
x + 3 = 3y + 9
x – 3y = 9–3
x – 3y = 6 …(ii)
x = 3y + 6
Putting, y = –2,–1 and 0, we get
x = 3 × – 2 + 6 = –6 + 6 =0
x = 3 × – 1 + 6 = –3 + 6 = 3
x = 3 × 0 + 6 = 0 + 6 = 6
Algebraic representation
From equation (i) and (ii)
x – 7y = – 42 …(i)
x – 3y = 6 …(ii)
Graphical representation
2. The coach of a cricket team buys 3 bats and 6 balls for Rs 3900. Later, she buys another bat and 3 more balls of the same kind for Rs 1300. Represent this situation algebraically and geometrically.
Solution:
Let cost of one bat = Rs x
Cost of one ball = Rs y
3 bats and 6 balls for Rs 3900 So that
3x + 6y = 3900 … (i)
Dividing equation by 3, we get
x + 2y = 1300
Subtracting 2y both side we get
x = 1300 – 2y
Putting y = –1300, 0 and 1300 we get
x = 1300 – 2 (–1300) = 1300 + 2600 = 3900
x = 1300 –2(0) = 1300 – 0 = 1300
x = 1300 – 2(1300) = 1300 – 2600 = – 1300
Given that she buys another bat and 2 more balls of the same kind for Rs 1300
So, we get
x + 2y = 1300 … (ii)
Subtracting 2y both side we get
x = 1300 – 2y
Putting y = – 1300, 0 and 1300 we get
x = 1300 – 2 (–1300) = 1300 + 2600 = 3900
x = 1300 – 2 (0) = 1300 – 0 = 1300
x = 1300 – 2(1300) = 1300 – 2600 = –1300
Algebraic representation
3x + 6y = 3900 … (i)
x + 2y = 1300 … (ii)
Graphical representation,
3. The cost of 2 kg of apples and 1 kg of grapes on a day was found to be Rs 160. After a month, the cost of 4 kg of apples and 2 kg of grapes is Rs 300. Represent the situation algebraically and geometrically.
Solution:
Let cost each kg of apples = Rs x
Cost of each kg of grapes = Rs y
Given that the cost of 2 kg of apples and 1kg of grapes on a day was found to be Rs 160
So that
2 x + y = 160 … (i)
2x = 160 - y
x = (160 – y)/2
Let y = 0 , 80 and 160, we get
x = (160 – ( 0 )/2 = 80
x = (160 – 80 )/2 = 40
x = (160 – 2 × 80)/2 = 0
Given that the cost of 4 kg of apples and 2 kg of grapes is Rs 300
So we get
4x + 2y = 300 … (ii)
Dividing by 2 we get
2x + y = 150
Subtracting 2x both side, we get
y = 150 – 2x
Putting x = 0 , 50 , 100 we get
y = 150 – 2 × 0 = 150
y = 150 – 2 × 50 = 50
y = 150 – 2 × (100) = –50
Algebraic representation,
2x + y = 160 … (i)
4x + 2y = 300 … (ii)
Graphical representation,
Exercise 3.2:
1. Form the pair of linear equations in the following problems, and find their solutions graphically.
(i) 10 students of Class X took part in a Mathematics quiz. If the number of girls is 4 more than the number of boys, find the number of boys and girls who took part in the quiz.
Solution:
Let number of boys = x
Number of girls = y
Given that total number of student is 10 so that
x + y = 10
Subtract y both side we get
x = 10 – y
Putting y = 0 , 5, 10 we get
x = 10 – 0 = 10
x = 10 – 5 = 5
x = 10 – 10 = 0
Given that If the number of girls is 4 more than the number of boys
So that
y = x + 4
Putting x = –4, 0, 4, and we get
y = – 4 + 4 = 0
y = 0 + 4 = 4
y = 4 + 4 = 8
Graphical representation
Both lines intersect at (3,7)
Hence the number of boys = 3 and number of girls = 7.
(ii) 5 pencils and 7 pens together cost Rs 50, whereas 7 pencils and 5 pens together cost Rs 46. Find the cost of one pencil and that of one pen.
Solution:
Let cost of pencil = Rs x
Cost of pens = Rs y
5 pencils and 7 pens together cost Rs 50,
So we get
5x + 7y = 50
Subtracting 7y both sides we get
5x = 50 – 7y
Dividing by 5 we get
Putting value of y = 5 , 10 and 15 we get
x = 10 – 7 × 5/5 = 10 – 7 = 3
x = 10 – 7 × 10/5 = 10 – 14 = – 4
x = 10 – 7 × 15/5 = 10 – 21 = – 11
Given that 7 pencils and 5 pens together cost Rs 46
7x + 5y = 46
Subtracting 7x both side we get
5y = 46 – 7x
Dividing by 5 we get
y = 9.2 – 1.4x
Putting x = 0 , 2 and 4 we get
y = 9.2 – 1.4 × 0 = 9.2 – 0 = 9.2
y = 9.2 – 1.4 (2) = 9.2 – 2.8 = 6.4
y = 9.2 – 1.4 (4) = 9.2 – 5.6 = 3.6
Graphical representation:
Both lines intersect at (3,5)
Hence the cost of one pencil = Rs 3 and cost of one pen = Rs 5.
2. On comparing the ratios a1/a2 , b1/b2 and c1/c2, find out whether the lines representing the following pairs of linear equations intersect at a point, are parallel or coincident.
(i) 5x – 4y + 8 = 0
7x + 6y – 9 = 0
Solution:
Comparing these equation with
a1x + b1y + c1 = 0
a2x + b2y + c2 = 0
We get
a1 = 5, b1 = –4, and c1 = 8
a2 =7, b2 = 6 and c2 = –9
a1/a2 = 5/7,
b1/b2 = –4/6 and
c1/c2 = 8/-9
Hence, a1/a2 ≠ b1/b2
Therefore, both are intersecting lines at one point.
(ii) 9x + 3y + 12 = 0
18x + 6y + 24 = 0
Comparing these equations with
a1x + b1y + c1 = 0
a2x + b2y + c2 = 0
We get
a1 = 9, b1 = 3, and c1 = 12
a2 = 18, b2 = 6 and c2 = 24
a1/a2 = 9/18 = 1/2
b1/b2 = 3/6 = 1/2 and
c1/c2 = 12/24 = 1/2
Hence, a1/a2 = b1/b2 = c1/c2
Therefore, both lines are coincident.
(iii) 6x – 3y + 10 = 0
2x – y + 9 = 0
Comparing these equations with
a1x + b1y + c1 = 0
a2x + b2y + c2 = 0
We get
a1 = 6, b1 = –3, and c1 = 10
a2 = 2, b2 = –1 and c2 = 9
a1/a2 = 6/2 = 3/1
b1/b2 = –3/–1 = 3/1 and
c1/c2 = 12/24 = 1/2
Hence, a1/a2 = b1/b2 ≠ c1/c2
Therefore, both lines are parallel.
3. On comparing the ratios a1/a2 , b1/b2 and c1/c2 find out whether the following pair of linear equations are consistent, or inconsistent.
(i) 3x + 2y = 5 ; 2x – 3y = 7
(ii) 2x – 3y = 8 ; 4x – 6y = 9
(iii) 3/2x + 5/3y = 7 ; 9x – 10y = 14
(iv) 5x – 3y = 11 ; – 10x + 6y = –22
(v) 4/3x + 2y =8 ; 2x + 3y = 12
Solution:
(i)
3x + 2y = 5 ; 2x – 3y = 7
a1/a2 = 3/2
b1/b2 = –2/3 and
c1/c2 = 5/7
Hence, a1/a2 ≠ b1/b2
These linear equations are intersecting each other at one point and thus have only one possible solution. Hence, the pair of linear equations is consistent.
(ii)
2x – 3y = 8 ; 4x – 6y = 9
a1/a2 = 2/4 = 1/2
b1/b2 = –3/–6 = 1/2 and
c1/c2 = 8/9
Hence, a1/a2 = b1/b2 ≠ c1/c2
Therefore, these linear equations are parallel to each other and thus have no possible solution. Hence, the pair of linear equations is inconsistent.
(iii)
3/2x + 5/3y = 7 ; 9x – 10y = 14
a1/a2 = 3/2/9 = 1/6
b1/b2 = 5/3/–10 = –1/6 and
c1/c2 = 7/14 = 1/2
Hence, a1/a2 ≠ b1/b2
Therefore, these linear equations are intersecting each other at one point and thus have only one possible solution. Hence, the pair of linear equations is consistent.
(iv)
5x – 3y = 11 ; – 10x + 6y = –22
a1/a2 = 5/-10 = -1/2
b1/b2 = -3/6 = -1/2 and
c1/c2 = 11/-22 = -1/2
Hence, a1/a2 = b1/b2 = c1/c2
Therefore, these linear equations are coincident pair of lines and thus have infinite number of possible solutions. Hence, the pair of linear equations is consistent.
(v)
4/3x + 2y =8 ; 2x + 3y = 12
a1/a2 = 4/3/2 = 2/3
b1/b2 = 2/3 and
c1/c2 = 8/12 = 2/3
Hence, a1/a2 = b1/b2 = c1/c2
Therefore, these linear equations are coincident pair of lines and thus have infinite number of possible solutions. Hence, the pair of linear equations is consistent.
4. Which of the following pairs of linear equations are consistent/inconsistent? If consistent, obtain the solution graphically:
(i) x + y = 5, 2x + 2y = 10
(ii) x – y = 8, 3x – 3y = 16
(iii) 2x + y – 6 = 0, 4x – 2y – 4 = 0
(iv) 2x – 2y – 2 = 0, 4x – 4y – 5 = 0
Solution:
x + y = 5; 2x + 2y = 10
a1/a2 = 1/2
b1/b2 = 1/2 and
c1/c2 = 5/10 = 1/2
Hence, a1/a2 = b1/b2 = c1/c2
Therefore, these linear equations are coincident pair of lines and thus have infinite number of possible solutions. Hence, the pair of linear equations is consistent.
x + y = 5
x = 5 – y
And, 2x + 2y = 10
x = 10 – 2y/2
Graphical representation:
(ii)
x – y = 8, 3x – 3y = 16
a1/a2 = 1/3
b1/b2 = –1/–3 = 1/3 and
c1/c2 = 8/16 = 1/2
Hence, a1/a2 = b1/b2 ≠ c1/c2
Therefore, these linear equations are parallel to each other and thus have no possible solution. Hence, the pair of linear equations is inconsistent.
(iii)
2x + y – 6 = 0, 4x – 2y – 4 = 0
a1/a2 = 2/4 = 1/2
b1/b2 = –1/2 and
c1/c2 = –6/–4 = 3/2
Hence, a1/a2 ≠ b1/b2
Therefore, these linear equations are intersecting each other at one point and thus have only one possible solution. Hence, the pair of linear equations is consistent.
2x + y – 6 = 0
y = 6 – 2x
And, 4x – 2y – 4 = 0
y = 4x – 4/2
Graphical representation:
From the figure, it can be observed that these lines are intersecting each other at the only one point i.e., (2,2) which is the solution for the given pair of equations.
(iv)
2x – 2y – 2 = 0, 4x – 4y – 5 = 0
a1/a2 = 2/4 = 1/2
b1/b2 = –2/–4 = 1/2 and
c1/c2 = 2/5
Hence, a1/a2 = b1/b2 ≠ c1/c2
Therefore, these linear equations are parallel to each other and thus, have no possible solution. Hence, the pair of linear equations is inconsistent.
5. Half the perimeter of a rectangular garden, whose length is 4 m more than its width, is 36 m. Find the dimensions of the garden.
Solution:
Let length of rectangle = x m
Width of the rectangle = y m
According to the question,
y – x = 4 ... (i)
y + x = 36 ... (ii)
y – x = 4
y = x + 4
y + x = 36
Graphical representation:
From the figure, it can be observed that these lines are intersecting each other at only point i.e., (16, 20). Therefore, the length and width of the given garden is 20 m and 16 m respectively.
6. Given the linear equation 2x + 3y – 8 = 0, write another linear equations in two variables such that the geometrical representation of the pair so formed is:
(i) intersecting lines
(ii) parallel lines
(iii) coincident lines
Solution:
(i) Intersecting lines:
For this condition,
a1/a2 ≠ b1/b2
The second line such that it is intersecting the given line is
2x + 4y – 6 = 0 as
a1/a2 = 2/2 = 1
b1/b2 = 3/4 and
a1/a2 ≠ b1/b2
(ii) Parallel lines
For this condition,
a1/a2 = b1/b2 ≠ c1/c2
Hence, the second line can be
4x + 6y – 8 = 0 as
a1/a2 = 2/4 = 1/2
b1/b2 = 3/6 = 1/2 and
c1/c2 = –8/–8 = 1
and a1/a2 = b1/b2 ≠ c1/c2
(iii) Coincident lines
For coincident lines,
a1/a2 = b1/b2 = c1/c2
Hence, the second line can be
6x + 9y – 24 = 0 as
a1/a2 = 2/6 = 1/3
b1/b2 = 3/9 = 1/3 and
c1/c2 = –8/–24 = 1/3
and a1/a2 = b1/b2 = c1/c2
7. Draw the graphs of the equations x – y + 1 = 0 and 3x + 2y – 12 = 0. Determine the coordinates of the vertices of the triangle formed by these lines and the x-axis, and shade the triangular region.
Answer
x – y + 1 = 0
x = y – 1
3x + 2y – 12 = 0
x = 12 – 2y/3
Graphical representation:
